现在位置: 首页 / CPU周常 / 技术分享 / 正文

两种最经典的最小生成树算法：Prim 与 Kruskal

  • GentleLijie
  • CPU周常
  • 2025-12-16
  • 132热度
  • 0评论

更好的呈现效果请移步: https://106.12.60.181:5000/mst.html 。

如果你对相关概念没有基本的了解，请参考: https://106.12.60.181:5000/mst-basic.html

在 \rm Year1\ CELEN086\ Algorithm 中有提及这两种最小生成树算法的简单逻辑，我们在此对其进行进一步展开，并提供简单的代码实现。

最小生成树(MST)是图论里那种“你可能没听过名字，但一定见过它的影子”的算法。无论是网络布线、道路规划，还是机器学习里的聚类分析，它都在默默发挥作用。

如果你想系统地理解 MST，那么 Prim 和 Kruskal 是绕不过去的两位主角。它们思路不同、适用场景不同，但都非常经典。

最小生成树到底是什么? 为什么要“最小”?

对于生成树的定义: 我们引用讲师 Manish Dhyani 提供的定义:

A spanning tree is a subset of a connected and undirected graph, which has all vertices covered with minimum possible number of edges.

生成树是连通图和无向图的子集，其所有顶点都覆盖了最小可能的边数。

更精确的定义是:

  • 设无向加权图为 G=(V,E,w)，生成树为包含 V 且无环的边集合 T\subseteq E。最小生成树是使 w(T)=\sum_{e\in T}w(e) 最小的生成树。
  • 割(cut)性质: 对于任意顶点划分 (S, V\setminus S)，跨割的最小权边必属于某个最小生成树；环(cycle)性质: 对于任一环，环中权重最大的边不属于某个最小生成树。这两条性质是证明 Prim 与 Kruskal 正确性的基础(参见文献[1])。

如果把一个连通图想象成城市地图:

  • 节点 = 城市
  • 边 = 城市之间的道路
  • 权重 = 修路成本

那么:

  • 生成树: 能让所有城市互相连通、但不出现环的道路集合
  • 最小生成树: 在所有生成树中，总成本最低的那一棵

Prim: 从一个点开始，像树枝一样往外长

Prim 的思路非常直观:
从一个点出发，每次挑一条最便宜的“跨界边”，把新点加入树中。

更形象一点:

你站在森林里的一棵树旁，每次都挑最近的一根树枝继续往外爬，最终你会爬满整棵树。

Prim 的流程

  1. 随便选一个起点
  2. 把它加入“已访问集合”
  3. 在所有连接“已访问集合”与“未访问集合”的边里，挑最便宜的一条
  4. 把对应的点加入已访问集合
  5. 重复直到所有点都加入

Prim 的特点是:

  • 像“点扩展”
  • 在稠密图(边很多)中更快

Prim 步骤

以下面这张图为例:

示意图

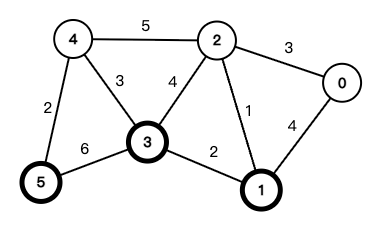
Prim 算法遍历步骤

步骤 已访问 Vis 选中节点 u 选中边 $\mathrm{dist}$ 向量 $\mathrm{parent}$ 向量 MST 边(按顺序) 累计权重
初始 ${}$ - - $[0, \infty, \infty, \infty, \infty, \infty]$ $[-, -, -, -, -, -]$ $[]$ 0
1 ${0}$ 0 — $[0, 4, 3, \infty, \infty, \infty]$ $[-, 0, 0, -, -, -]$ $[]$ 0
2 ${0,2}$ 2 $0-2\ (3)$ $[0, 1, 3, 4, 5, \infty]$ $[-, 2, 0, 2, 2, -]$ $[0-2(3)]$ 3
3 ${0,2,1}$ 1 $2-1\ (1)$ $[0, 1, 3, 2, 5, \infty]$ $[-, 2, 0, 1, 2, -]$ $[0-2(3),\ 2-1(1)]$ 4
4 ${0,2,1,3}$ 3 $1-3\ (2)$ $[0, 1, 3, 2, 3, 6]$ $[-, 2, 0, 1, 3, 3]$ $[0-2(3),\ 2-1(1),\ 1-3(2)]$ 6
5 ${0,2,1,3,4}$ 4 $3-4\ (3)$ $[0, 1, 3, 2, 3, 2]$ $[-, 2, 0, 1, 3, 4]$ $[0-2(3),\ 2-1(1),\ 1-3(2),\ 3-4(3)]$ 9
6 ${0,2,1,3,4,5}$ 5 $4-5\ (2)$ $[0, 1, 3, 2, 3, 2]$ $[-, 2, 0, 1, 3, 4]$ $[0-2(3),\ 2-1(1),\ 1-3(2),\ 3-4(3),\ 4-5(2)]$ 11

✅ Prim 的 Python 实现

邻接矩阵的 Prim 算法

import sys

def prim(adj):
    n = len(adj)
    visited = [False] * n
    dist = [sys.maxsize] * n
    parent = [-1] * n

    dist[0] = 0  # 从 0 号点开始

    for _ in range(n):
        # 找到未访问点中 dist 最小的
        u = -1
        for i in range(n):
            if not visited[i] and (u == -1 or dist[i] < dist[u]):
                u = i

        visited[u] = True

        # 更新相邻节点的距离
        for v in range(n):
            if adj[u][v] != 0 and not visited[v] and adj[u][v] < dist[v]:
                dist[v] = adj[u][v]
                parent[v] = u

    return parent

Kruskal: 从最便宜的边开始买起

如果说 Prim 是“从点往外扩展”，那么 Kruskal 就是“从边往里挑选”。

Kruskal 的流程

  1. 把所有边按权重从小到大排序
  2. 从最便宜的边开始尝试加入
  3. 如果加入后不成环，就收下
  4. 直到选够 n-1 条边

并查集(Union-Find)在这里的作用

并查集负责判断“加入这条边会不会成环”。

  • 如果两个点已经在同一个集合里 → 加这条边会成环 → 不能要
  • 否则就把两个集合合并

Kruskal 的特点是:

  • 在稀疏图(边少)中更快

Kruskal 步骤

示意图

已排序的边(权重从小到大，0-based):

  1. $1\text{-}2\ (1)$
  2. $1\text{-}3\ (2)$
  3. $4\text{-}5\ (2)$
  4. $0\text{-}2\ (3)$
  5. $3\text{-}4\ (3)$
  6. $0\text{-}1\ (4)$
  7. $2\text{-}3\ (4)$
  8. $2\text{-}4\ (5)$
  9. $3\text{-}5\ (6)$

Kruskal 算法遍历步骤

步骤 当前考虑边 并查集状态(集合划分) 是否加入 MST 边(按顺序) 累计权重
1 $1\text{-}2\ (1)$ ${1,2},\ {0},\ {3},\ {4},\ {5}$ 是 $[1\text{-}2(1)]$ 1
2 $1\text{-}3\ (2)$ ${1,2,3},\ {0},\ {4},\ {5}$ 是 $[1\text{-}2(1),\ 1\text{-}3(2)]$ 3
3 $4\text{-}5\ (2)$ ${1,2,3},\ {0},\ {4,5}$ 是 $[1\text{-}2(1),\ 1\text{-}3(2),\ 4\text{-}5(2)]$ 5
4 $0\text{-}2\ (3)$ ${0,1,2,3},\ {4,5}$ 是 $[1\text{-}2(1),\ 1\text{-}3(2),\ 4\text{-}5(2),\ 0\text{-}2(3)]$ 8
5 $3\text{-}4\ (3)$ ${0,1,2,3,4,5}$ 是 $[1\text{-}2(1),\ 1\text{-}3(2),\ 4\text{-}5(2),\ 0\text{-}2(3),\ 3\text{-}4(3)]$ 11
停止 已选 5 条边(n-1) 全部连通 — 同上 11

因此最终 MST 的总权重为:

w_{\mathrm{MST}} = 1 + 2 + 2 + 3 + 3 = 11.

✅ Kruskal 的 Python 实现 (邻接矩阵)

Kruskal 算法

def find(parent, x):
    if parent[x] != x:
        parent[x] = find(parent, parent[x])
    return parent[x]

def union(parent, rank, x, y):
    rx, ry = find(parent, x), find(parent, y)
    if rx != ry:
        if rank[rx] < rank[ry]:
            parent[rx] = ry
        elif rank[rx] > rank[ry]:
            parent[ry] = rx
        else:
            parent[ry] = rx
            rank[rx] += 1

def kruskal(adj):
    n = len(adj)
    edges = []

    # 从邻接矩阵提取边
    for i in range(n):
        for j in range(i + 1, n):
            if adj[i][j] != 0:
                edges.append((adj[i][j], i, j))

    edges.sort()  # 按权重排序

    parent = list(range(n))
    rank = [0] * n
    mst = []

    for w, u, v in edges:
        if find(parent, u) != find(parent, v):
            mst.append((u, v, w))
            union(parent, rank, u, v)

    return mst

(可选) 如果你想用二叉堆优化 Prim

Prim 常见的优化方式是用二叉堆(Binary Heap)作为优先队列，使得每次取最小边更快。

优势

  • 作为优先队列，能快速取出当前最小的候选边或候选顶点；适合用于 Prim 算法的“每次取最小跨界边”步骤。
  • 简单、易实现(Python 中可直接使用标准库 heapq)。

时间复杂度

  • 使用二叉堆实现的 Prim: 时间为 O(E\log V)(或更精确地说，所有边最多入堆一次，出堆最多 O(E) 次，堆操作为 O(\log V))，空间为 O(V+E)。这里 V=|V|, E=|E|。
  • 与之对比: 朴素的数组实现为 O(V^2)(适合稠密图)；若使用 Fibonacci 堆，理论上可达 O(E + V\log V)，但实现复杂且常数较大。

实现要点

  • 建议输入使用邻接表(adjacency list)，即 adj[u] = [(v, w), ...]，避免邻接矩阵在稀疏图上的低效。
  • 堆内放入元素形如 (weight, node, parent)，弹出时忽略已访问节点(lazy deletion)，同时更新 dist[node] 与 parent[node]。

注意:

  • 并查集 (Union-Find) : 在并操作中采用按秩(rank/size)合并并配合路径压缩，可将查找/合并的摊还复杂度降至近似常数。实现时注意初始 parent 与 rank 的设定以及递归或迭代实现的栈深度问题。
  • 优先队列 (用于 Prim) : 常用 Python 的 heapq 实现 lazy deletion(即当堆顶已被访问时跳过)，并保持一个 dist 数组以免重复处理无用的旧条目；若需要 decrease-key 的高效实现，可考虑支持 decrease-key 的堆结构(如 pairing heap 或手写索引堆)。

✅ 示例(Python)

二叉堆优化的 Prim 算法

import heapq

def prim_heap(adj, start=0):
    """邻接表输入: adj[u] = [(v, w), ...]。返回 (mst_edges, total_weight)。"""
    n = len(adj)
    visited = [False] * n
    dist = [float('inf')] * n
    parent = [-1] * n

    dist[start] = 0
    heap = [(0, start, -1)]  # (weight, node, parent)
    mst = []
    total = 0

    while heap:
        w, u, p = heapq.heappop(heap)
        if visited[u]:
            continue
        visited[u] = True
        parent[u] = p
        if p != -1:
            mst.append((p, u, w))
            total += w

        for v, wt in adj[u]:
            if not visited[v] and wt < dist[v]:
                dist[v] = wt
                heapq.heappush(heap, (wt, v, u))

    # 若图不连通，mst 中的边数会 < V-1，可视需要检查并处理
    return mst, total

Prim vs Kruskal: 到底怎么选?

特性和应用场景

Prim vs Kruskal: 特性和应用场景

特性 Prim Kruskal
思路 从点扩展 从边挑选
数据结构 优先队列(或简单数组) 并查集
适合图类型 稠密图 稀疏图
实现难度 中等 简单(排序 + 并查集)
直观理解 树枝生长 预算购物

时间复杂度对比

  • Prim (邻接矩阵 + 线性扫描) : O(V^2)，适用于稠密图或小规模图。
  • Prim (邻接表 + 二叉堆) : O(E\log V)，常用于稀疏图。
  • Prim (邻接表 + Fibonacci 堆) : 理论 O(E + V\log V)，实际实现复杂，常数较大。
  • Kruskal(边排序 + 并查集): 排序 O(E\log E)=O(E\log V)，并查集操作摊还近似常数 \alpha(n)。

另外，注意到两个算法均使用贪心思想。以下附上对其贪心正确性的简单证明:

  • Prim: 每一步选取跨割最小边，依据割性质，该选择不会丧失全局可行最优解；通过归纳可证明最终得到 MST。
  • Kruskal: 设当前选边集合为 A，考虑排序后的最小可行边 e，若最优解不包含 e，可用交换论证(replace 最大权边于对应环)得到不更差的解，从而说明选 e 不影响最优性。

总结

Prim 和 Kruskal 是最小生成树的两种经典算法:

  • Prim: 从点出发，逐步扩展
  • Kruskal: 从边出发，逐条挑选
  • 稠密图用 Prim，稀疏图用 Kruskal
  • 两者都非常适合教学、竞赛和工程实践

如果你正在学习图论，这两个算法绝对值得自己动手实现一遍。理解它们的过程，也能帮助你更好地理解“图”这种结构本身的美感。

参考文献

[1] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein. Introduction to Algorithms[M]. 3rd ed. Cambridge: MIT Press, 2009.

[2] Prim R. C. Shortest connection networks and some generalizations[J]. Bell System Technical Journal, 1957, 36(6):1389-1401.

[3] Kruskal J. B. On the shortest spanning subtree of a graph and the traveling salesman problem[J]. Proceedings of the American Mathematical Society, 1956, 7:48-50.

[4] Tarjan R. E. Efficiency of a good but not linear set union algorithm[J]. Journal of the ACM, 1975, 22(2):215-225.

[5] Fredman M. L., Tarjan R. E. Fibonacci heaps and their uses in improved network optimization algorithms[J]. Journal of the ACM, 1987, 34(3):596-615.

[6] 作者博客. 两种最经典的最小生成树算法: Prim 与 Kruskal[EB/OL]. http://106.12.60.181/2025/12/16/%E4%B8%A4%E7%A7%8D%E6%9C%80%E7%BB%8F%E5%85%B8%E7%9A%84%E6%9C%80%E5%B0%8F%E7%94%9F%E6%88%90%E6%A0%91%E7%AE%97%E6%B3%95%EF%BC%9APrim-%E4%B8%8E-Kruskal/, 2025-12-16.