乡村公路连通计划:Prim vs Kruskal
- CPU周常
- 2025-12-16
- 94热度
- 0评论
更好的呈现效果请移步: https://106.12.60.181:5000/mst_basic.html
本文更着重进行故事化的讲解,对于代码实现和具体功能链的展开,请参考这篇推文:https://106.12.60.181:5000/mst.html
在 \rm Year1\ CELEN086\ Algorithm 中有提及这两种最小生成树算法的简单逻辑,我们在此对其进行进一步展开,并提供简单的代码实现。
最小生成树(MST)是图论里那种“你可能没听过名字,但一定见过它的影子”的算法。无论是网络布线、道路规划,还是机器学习里的聚类分析,它都在默默发挥作用。
在此,我们用一个故事化的场景,展开两种最小生成树算法的执行过程。
📍 场景设定
在一个美丽的山谷里,有6个村庄(编号0-5)。村长决定修建公路,让所有村庄都能互相连通。每两个村庄之间的修路成本如下:
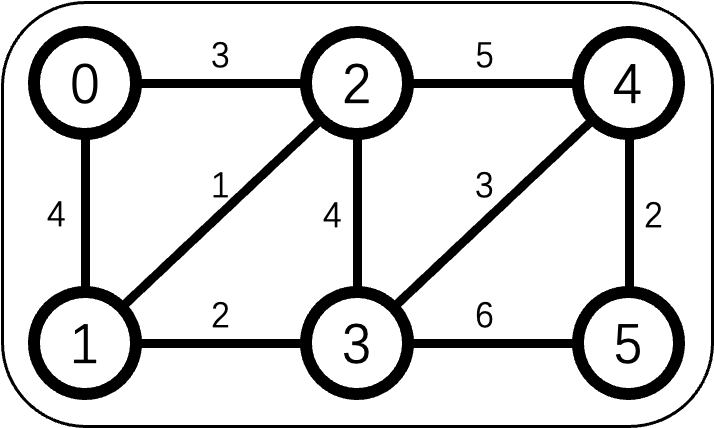
总预算有限,村长需要找到总成本最低的修路方案。
🎯 Prim 的修路策略:从中心向外扩张
村长选择了 Prim 方案——从一个村庄开始,逐步向外延伸。
Day 1
村长站在0号村,派勘察队测量:
- 去1号村:4万
- 去2号村:3万(最便宜)
✅ 先修 0-2 公路(3万),2号村加入“已连通”区域。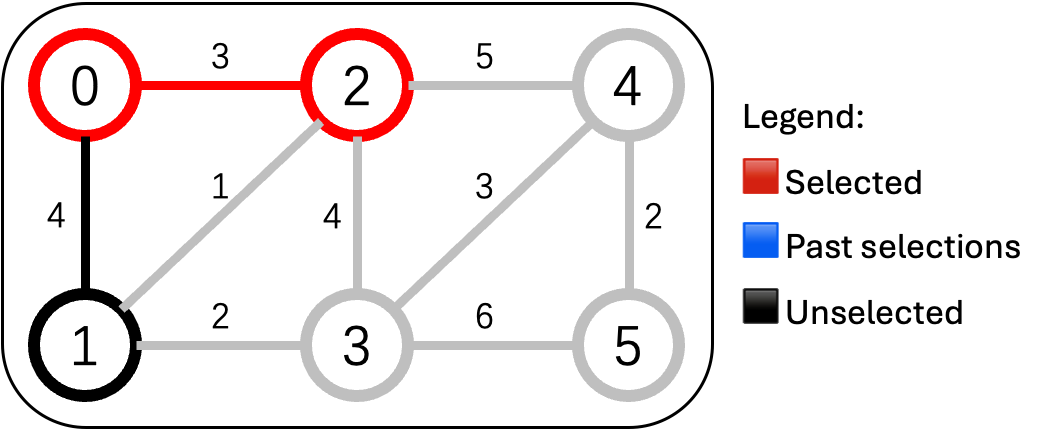
Day 2
现在已连通区域:{0, 2}。勘察队从这两个村出发:
- 0-1:4万
-
2-1:1万(最便宜)
-
2-3:4万
-
2-4:5万
✅ 修 2-1 公路(1万),1号村加入。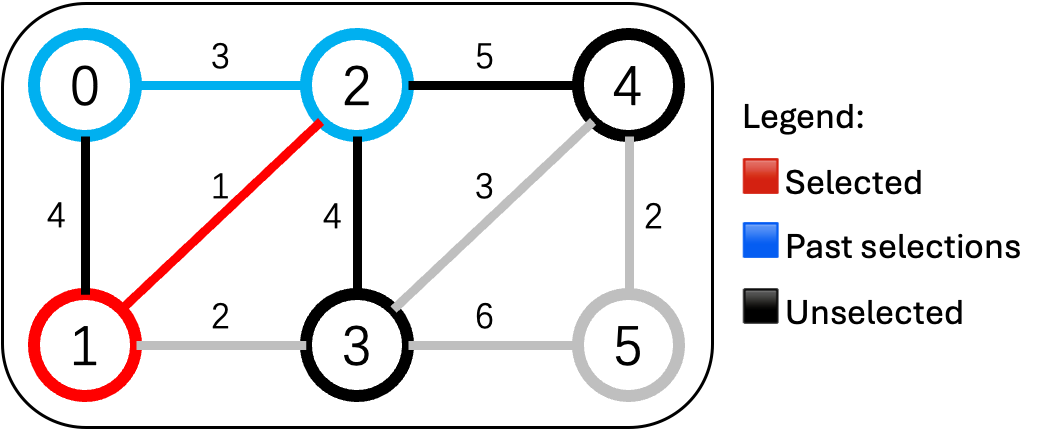
Day 3
已连通:{0,1,2}。勘察:
- 1-3:2万(最便宜)
- 2-3:4万
-
2-4:5万
✅ 修 1-3 公路(2万),3号村加入。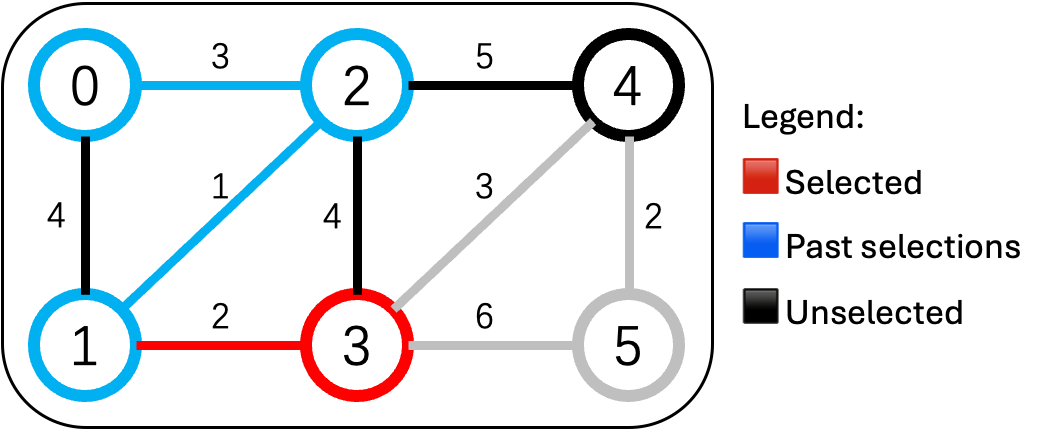
Day 4
已连通:{0,1,2,3}。勘察:
- 3-4:3万(最便宜)
-
3-5:6万
✅ 修 3-4 公路(3万),4号村加入。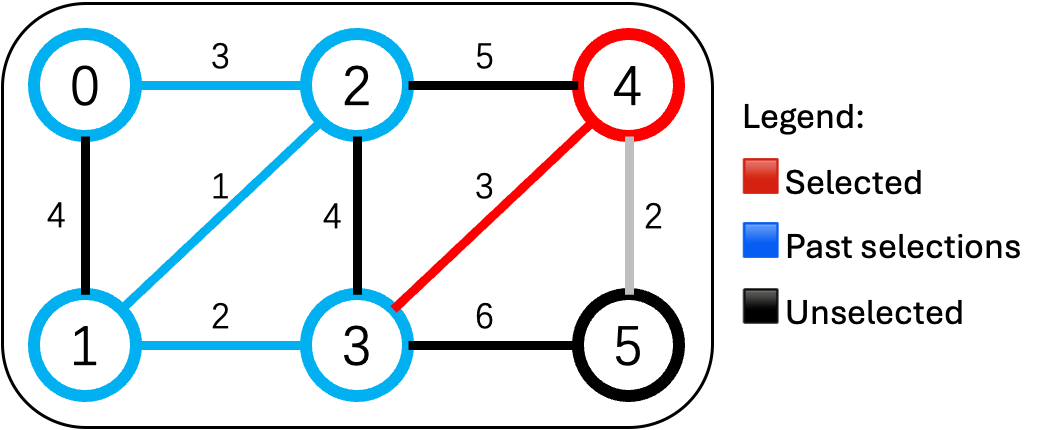
Day 5
已连通:{0,1,2,3,4}。勘察:
- 4-5:2万(最便宜)
✅ 修 4-5 公路(2万),5号村加入。
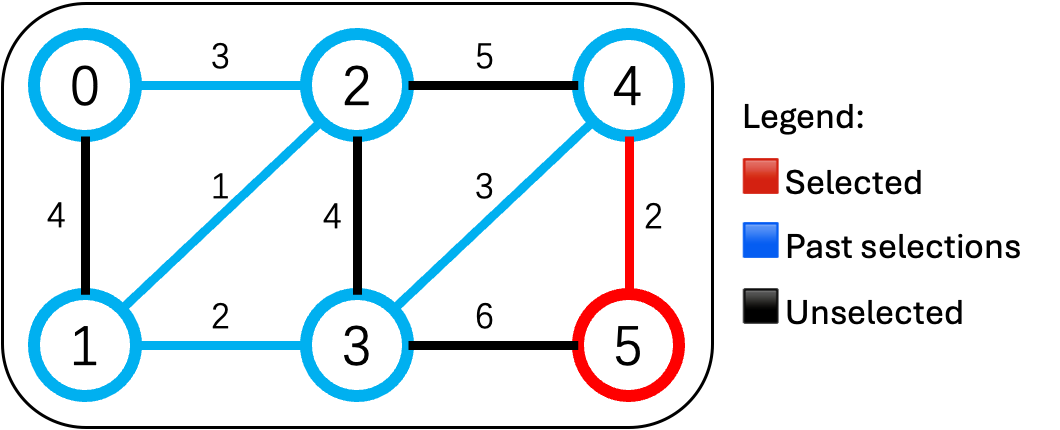
🎉 完成!
总成本:3 + 1 + 2 + 3 + 2 = 11万元
修路顺序:0-2 → 2-1 → 1-3 → 3-4 → 4-5
🎯 Kruskal 的修路策略:从便宜的开始买
村长换了个思路,用 Kruskal 方案——把所有可能的路按成本排序,从最便宜的开始选。
Step 1
把9条路按成本排序:
1️⃣ 1-2村:1万
2️⃣ 1-3村:2万
3️⃣ 4-5村:2万
4️⃣ 0-2村:3万
5️⃣ 3-4村:3万
6️⃣ 0-1村:4万
7️⃣ 2-3村:4万
8️⃣ 2-4村:5万
9️⃣ 3-5村:6万
Step 2
开始挑选(每次选最便宜的,且不会形成“环状”路线):
- ✅ 修 1-2(1万) —— 连接了1号和2号村
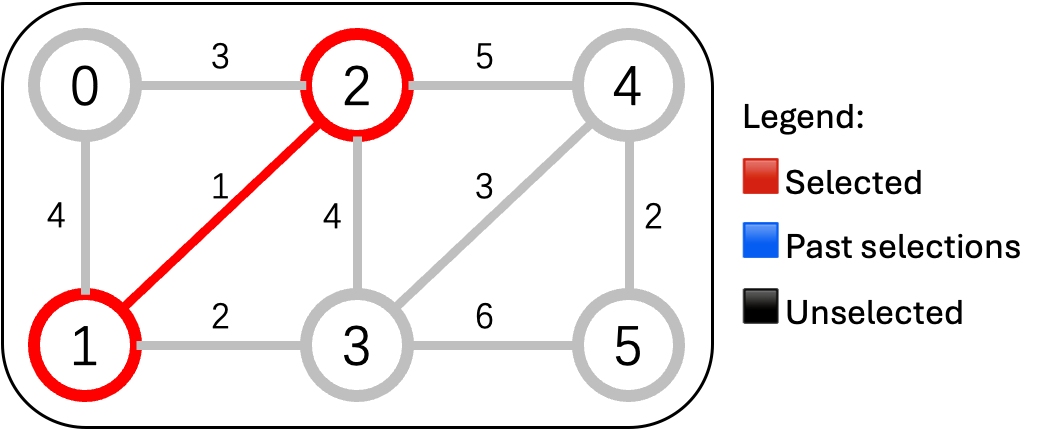
-
✅ 修 1-3(2万) —— 连接了3号村
✅ 修 4-5(2万) —— 连接了4号和5号村
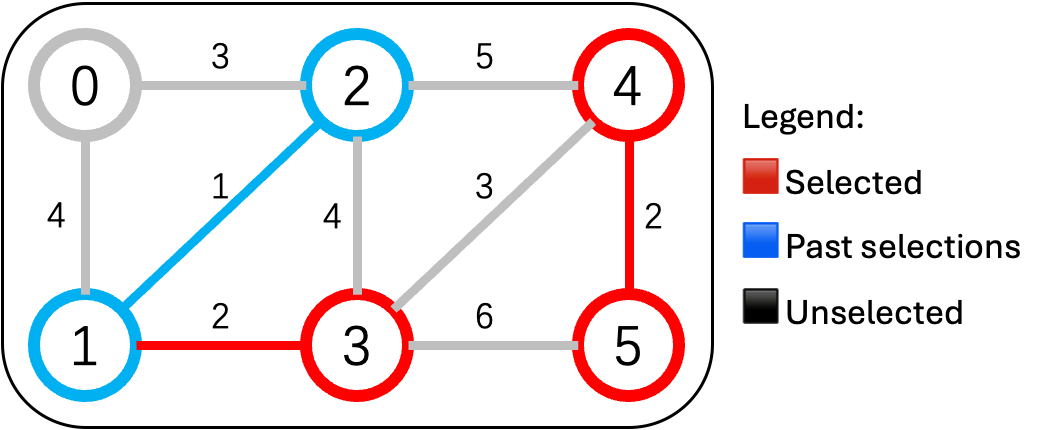
-
✅ 修 0-2(3万) —— 连接了0号村
-
✅ 修 3-4(3万) —— 连接了最后两个区域
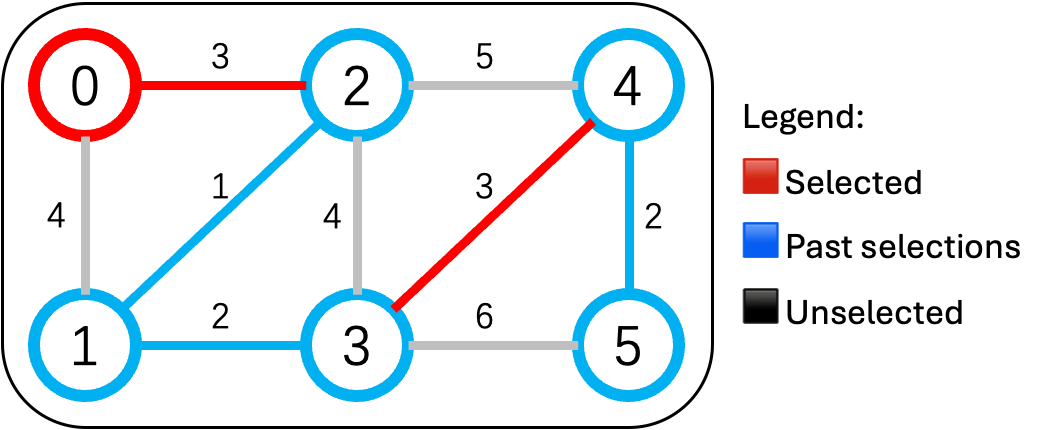
注意: 当考虑第6条路(0-1,4万)时,发现0和1已经在同一个连通区域了(通过0-2-1),修这条路会形成“环”,浪费钱,所以不修。
Step 3
已经修了5条路(6个村需要5条路),所有村庄连通!
🎉 完成!
总成本:1 + 2 + 2 + 3 + 3 = 11万元
修路顺序:1-2 → 1-3 → 4-5 → 0-2 → 3-4
🤔 两种方法的对比观察
两种方法的对比观察
| 对比点 | Prim(生长法) | Kruskal(购物法) |
|---|---|---|
| 起点 | 必须从某个村开始(如0号) | 从最便宜的路开始,不关心起点 |
| 思考方式 | “我现在在哪儿?最近的陌生村是哪个?” | “所有路里,哪条最便宜且有用?” |
| 关键操作 | 每次找连接“已连通”和“未连通”的最便宜路 | 按价格排序,逐条检查是否成环 |
| 最终结果 | 总成本相同(11万),但修路顺序不同 | 总成本相同,路的选择也相同 |
有趣的是:虽然两种方法思考角度不同,修路顺序不同,但它们最终选出的5条路完全一样,总成本也相同。这说明最优解是唯一的,但到达最优解的路径可以有多条。
下次当你面临“如何用最少成本连接多个点”的问题时,不妨想想:我是应该像树枝一样生长(Prim),还是像购物一样挑选(Kruskal)?
最小生成树到底是什么? 为什么要“最小”?
对于生成树的定义: 我们引用讲师 Manish Dhyani 提供的定义:
A spanning tree is a subset of a connected and undirected graph, which has all vertices covered with minimum possible number of edges.
生成树是连通图和无向图的子集,其所有顶点都覆盖了最小可能的边数。
更精确的定义是:
- 设无向加权图为 G=(V,E,w),生成树为包含 V 且无环的边集合 T\subseteq E。最小生成树是使 w(T)=\sum_{e\in T}w(e) 最小的生成树。
- 割(cut)性质: 对于任意顶点划分 (S, V\setminus S),跨割的最小权边必属于某个最小生成树;环(cycle)性质: 对于任一环,环中权重最大的边不属于某个最小生成树。这两条性质是证明 Prim 与 Kruskal 正确性的基础(参见文献[1])。
如果把一个连通图想象成城市地图:
- 节点 = 城市
- 边 = 城市之间的道路
- 权重 = 修路成本
那么:
- 生成树: 能让所有城市互相连通、但不出现环的道路集合
- 最小生成树: 在所有生成树中,总成本最低的那一棵
Prim 的流程
- 随便选一个起点
- 把它加入“已访问集合”
- 在所有连接“已访问集合”与“未访问集合”的边里,挑最便宜的一条
- 把对应的点加入已访问集合
- 重复直到所有点都加入
Prim 的特点是:
- 像“点扩展”
- 在稠密图(边很多)中更快
Kruskal 的流程
- 把所有边按权重从小到大排序
- 从最便宜的边开始尝试加入
- 如果加入后不成环,就收下
- 直到选够 n-1 条边
时间复杂度对比
- Prim (邻接矩阵 + 线性扫描) : O(V^2),适用于稠密图或小规模图。
- Prim (邻接表 + 二叉堆) : O(E\log V),常用于稀疏图。
- Prim (邻接表 + Fibonacci 堆) : 理论 O(E + V\log V),实际实现复杂,常数较大。
- Kruskal(边排序 + 并查集): 排序 O(E\log E)=O(E\log V),并查集操作摊还近似常数 \alpha(n)。
另外,注意到两个算法均使用贪心思想。以下附上对其贪心正确性的简单证明:
- Prim: 每一步选取跨割最小边,依据割性质,该选择不会丧失全局可行最优解;通过归纳可证明最终得到 MST。
- Kruskal: 设当前选边集合为 A,考虑排序后的最小可行边 e,若最优解不包含 e,可用交换论证(replace 最大权边于对应环)得到不更差的解,从而说明选 e 不影响最优性。
总结
Prim 和 Kruskal 是最小生成树的两种经典算法:
- Prim: 从点出发,逐步扩展
- Kruskal: 从边出发,逐条挑选
- 稠密图用 Prim,稀疏图用 Kruskal
- 两者都非常适合教学、竞赛和工程实践
如果你正在学习图论,这两个算法绝对值得自己动手实现一遍。理解它们的过程,也能帮助你更好地理解“图”这种结构本身的美感。